1.14 Transformada de Fourier
Devido às dificuldades encontradas na medição, no
armazenamento e nos calculos envolvidos com as respostas ao impulso, procurou-se
um tratamento matemático que simplificasse a caracterização
dos dispositivos e o posterior processamento dos sinais. As transformadas
matemáticas têm por objetivo modificar o domínio de
uma função. Quando a transformada de Fourier é
aplicada a sinais elétricos, ocorre a transformação
da função do domínio do tempo para o domínio
da frequência.
-
g(t) é a representação do sinal no domínio
do tempo que é uma função real da variável
real t (tempo)
-
G(f) é a representação do mesmo sinal no domínio
da frequência que é uma função complexa
da variável real f (frequência)
-
g(t) « G(f) formam o par transformado
cuja relação é unívoca (duas funções
distintas no tempo não podem corresponder a uma mesma função
na frequência e vice-e-versa)
A transformada direta de Fourier fornece G(f) a partir de g(t)
através de
 (1-11) cuja unidade é W½ /
Hz.
(1-11) cuja unidade é W½ /
Hz.
A transformada inversa de Fourier fornece g(t) a partir de G(f)
através de
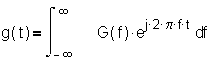 (1-12) cuja unidade é W½.
(1-12) cuja unidade é W½.
Nas equações acima t e f são as variáveis
tempo e frequência, respectivamente, e j = (-1)½
é a unidade imaginária.
A transformada de Fourier pode ser aplicada a sinais determinísticos
no domínio do tempo, sejam eles de duração finita
ou periódicos.
Universidade Federal do Paraná
- Departamento de Engenharia Elétrica
- www.eletr.ufpr.br/artuzi